PPP (complexity)
PPP is a complexity class, standing for "Polynomial Pigeonhole Principle". Introduced by Christos Papadimitriou in 1994[1] (page 528), PPP is a subclass of TFNP. It is a class of search problems that can be shown to be total by an application of the pigeonhole principle.
PPP is defined as follows. A function computation problem belongs to PPP if it admits a polynomial-time reduction to the problem PIGEONHOLE CIRCUIT, in which an input consists of a boolean circuit having the same number of input bits as output bits, and a solution consists of either an input vector that is mapped to the output 0, or alternatively two distinct input vectors that are mapped to the same output. Note that it is the pigeonhole principle that guarantees that a solution must exist. A problem is complete for the class PPP if in addition, PIGEONHOLE CIRCUIT is reducible to that problem.
PPP contains PPAD as a subclass. This is because the corresponding problem that defines PPAD, known as END OF THE LINE, can be reduced (in a straightforward way) to PIGEONHOLE CIRCUIT.
At present, the only problems known to be complete for PPP are variants of PIGEONHOLE CIRCUIT; this is a deficiency of PPP, since this means that it has so far failed to capture the complexity of additional problems. However, the definition of the class PPP highlights the way that the pigeonhole principle is a generalization of the "parity argument on a directed graph" principle that assures that search problems belonging to PPAD are indeed total. It is an open question whether EQUAL SUBSETS is complete for PPP, where EQUAL SUBSETS is defined as follows: The input consists of a set of  positive integers that add up to less than
positive integers that add up to less than 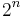 . The problem is to find two distinct subsets of these numbers that have the same total.
. The problem is to find two distinct subsets of these numbers that have the same total.